Our new paper titled “Quantum topological switch and controllable quasi 1D wires in antimonene”[1] is up in arxiv, and here is a brief summery of the big idea proposed there.

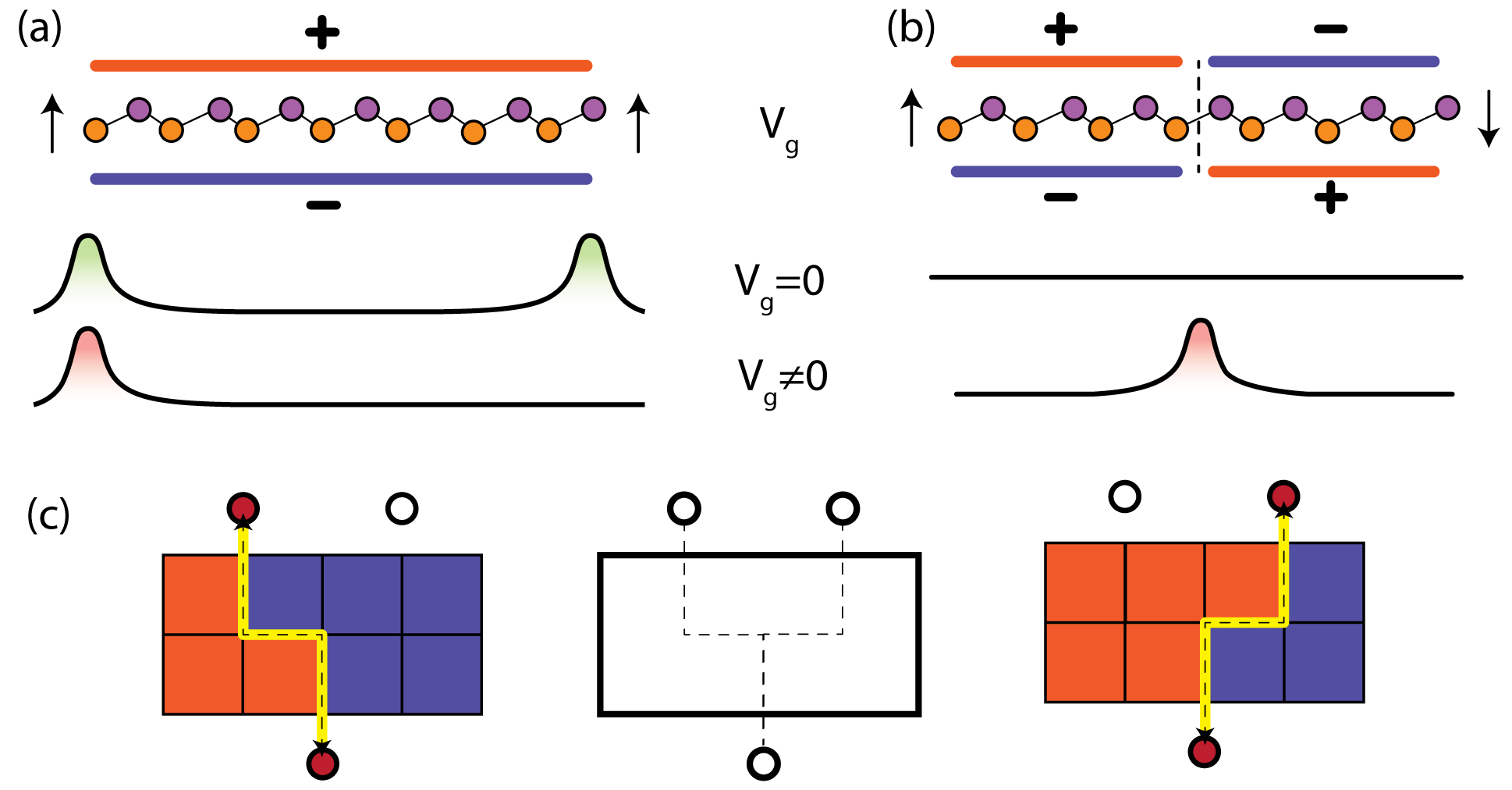
In our previous papers [2,3] we showed that a 2 Dimensional sheet of $p_x-p_y-p_z$ symmetry orbitals arranged in honeycomb lattice has very interesting effects, one of which is that the system is in a state of weak Topological Crystalline insulator. Although being weak is a misnomer and an interesting read is given here titled The strong side of weak topological insulators[4], the weakness of this system can be beautifully exploited. The protection of this weak surface state, in this system, is through the presence of inversion symmetry in the 2D system. Because of the buckled nature of the system, we show that applying a simple electric field perpendicular to the system (just like in case of gating) can break this inversion and thus gaps the surface state. This is shown in the figure (a). Second devices uses almost the same principle, but instead apply electric field locally breaking the inversion at different regions which we showed to create 1D channel pathways inside the system, this is shown in (b). This can in principle be used to design pixlated patches which can be used for configurable circuits that have unique 1D semi-conducting wire.

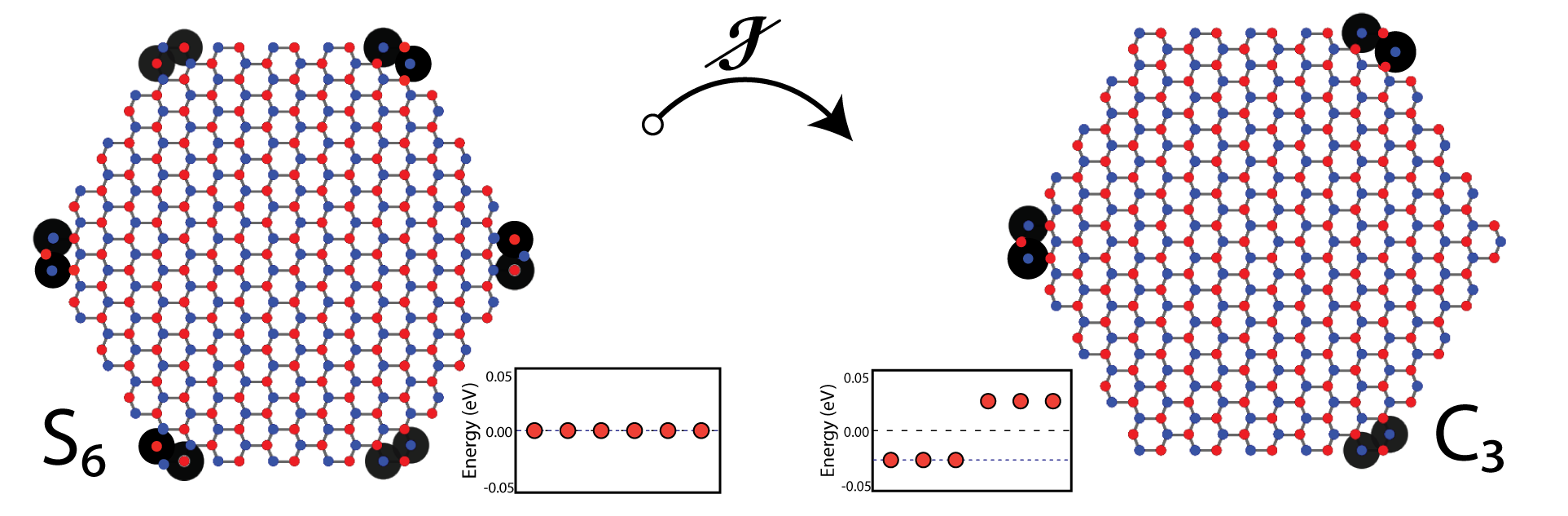
Secondly, in [3] we showed that this system is a Higher Order Topological Insulator (HOTI), again protected by inversion symmetry. Thus again breaking the symmetry in this system breaks the $S_6$ symmetry the system is into $C_3$. This forces the anomalous fractional charge excitations in $S_6$ (which exists in 6 corners) to disappear and concentrate in $C_3$ symmetric fashion (3 corners) This is shown bellow

References