Before 1980, the principle of broken symmetry was the key concept for the classification of states of matter. The discovery of quantum Hall effect by Klaus von Klitzing, started a new paradigm in physics by providing the first example of a quantum phase transition where no spontaneous symmetry was broken. The unique feature of these quantum phases is the fact that even though two ground states share the same symmetry, they still belong to different phases (i.e. cannot be continuously tuned to each other through a smooth deformation of the Hamiltonian). This is a result of the fact that the wave functions that are defined on the n-dimensional Brillouin zone are "knotted" in non-trivial ways, despite having the same symmetry.

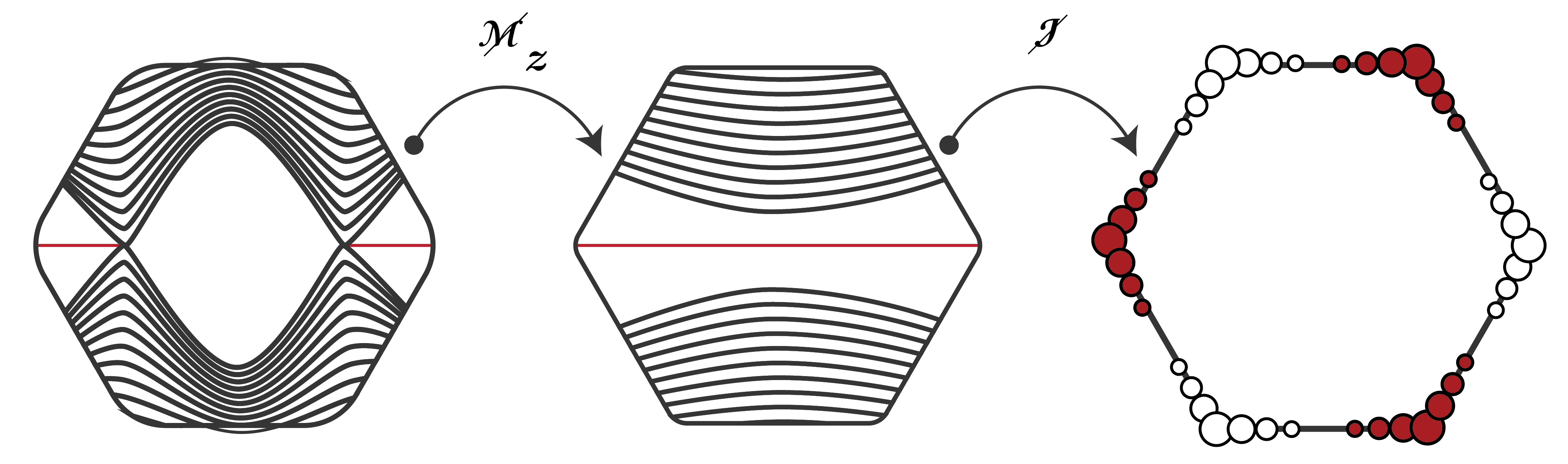
In this talk, we start by describing a symmetry enforced nodal line semi-metal (NLSM) in the 2D flat form of honeycomb Group - V and its non trivial thermo-electric response. We will then proceed to show that, upon buckling, the system undergoes its first phase transition from NLSM to 2 sets of oppositely wound unpinned Dirac cones protected by C₂ symmetry. Further buckling leads to these unpinned Dirac cones annihilating in pairs at two distinct critical angle leading to a second topological phase transition to an insulating state. We then show that this seemingly innocuous insulating state is indeed a weak topological crystalline insulator. Furthermore, upon closer look, this insulating state turns out to be a Higher Order Topological Insulator (HOTI) that is protected by S₆ symmetry. HOTIs are d-spatial dimensional systems featuring topologically protected gap-less states at their (d-n)-dimensional boundaries with d>1. In a broader context, we will see that the the topological properties of buckled Group - V stem from the fact that they topologically belong to the class of Obstructed Atomic Limit (OAL) insulators. Combining all these, we will prove that annihilating pairs of Dirac fermions necessitate a topological phase transition from the critical semi-metallic phase to an OAL insulator phase. We also uncover the rich set of phases in the phase diagram in case of annihilating Dirac fermions and study their entanglement properties using entanglement entropy. We will demonstrate that these phases can be distinguished by a Z₂xZ₂ invariant. Finally, based on the non-trivial topology of these systems, we propose the conceptual design of a quantized switch that is protected by topology and a mechanism to create configurable 1D wire channels by breaking the symmetry that is protecting the edge spectrum - the inversion (I).

Last part of the talk involves the remarkable discovery of a spin polarized 2D electron/hole gas at the surfaces of a well known system - LiCoO₂. By mapping the first-principles computational results to a minimal tight-binding model, we will show that these surface states are related to a non-chiral 3D generalization of the quadripartite Su-Schriefer-Heeger (SSH4) model and has a topological origin.