Research
For you live your life once, chose 'em projects wisely
Though my main PhD work is in theoretical and computational physics, my interests range from mathematical modeling of carnatic music to deep-learning. I am excited about anything that involves mathematics and dabble in them.
Feynman used to say that there were two kinds of physicists, the Babylonians and the Greeks. The Babylonians made civilization’s first great strides in understanding numbers and equations, but it was the Greeks whom we credit with inventing mathematics. Put simply, the Babylonians focused on the phenomenon, the Greeks on the underlying order.Feynman considered himself a Babylonian; Gell-Mann, Feynman’s contemporary, was more the Greek type, wanting to categorize nature and impose an efficient mathematical order on the underlying data. I would classify myself as the latter, the Greek. I am fascinated by the language of mathematics to describe, in most elegant way, the properties and rules of nature.
My PhD is mainly focused on working with a new phase of matter called Topological quantum systems. These are quantum systems(mostly materials), where interestingly, new particles that are analogous to fundamental particles emerge from collective excitations of electrons in low energy. These kind of “quasi-particles” give rise to intriguing effects in real materials. Other than studying these low energy excitations, my work also focuses on trying to describe systems where one cannot think of electrons as individual non-interacting electrons anymore. These systems are the so called strongly correlated systems. These kind of systems where our notion of Independent electron picture breaks down, has exotic phases that pop up as emergent phenomena like High temperature superconductivity, Spin Density waves etc..
Physics
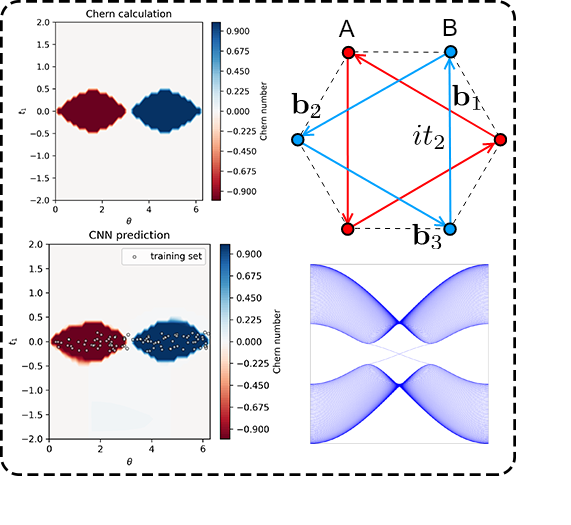
Machine Learning topological Z2 invarients: Learning wave functions as fiber bundles in a combined CNN+BRNN (Convolutional Neural Networks+Bidirectional Recurrent Neural Networks) architecture. Generalizations go beyond Haldene model and seems to extend well to disordered systems.
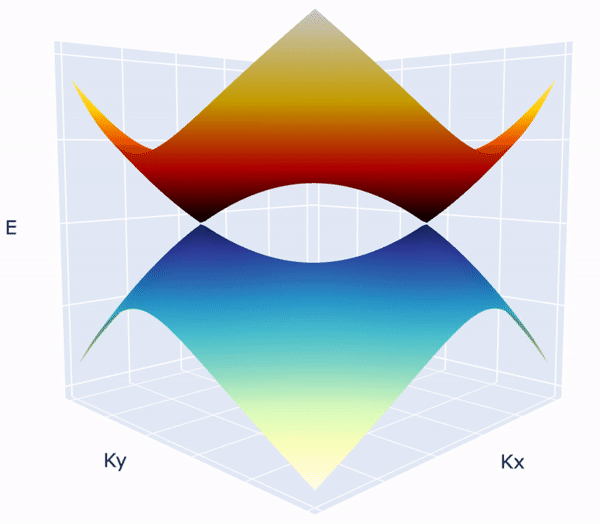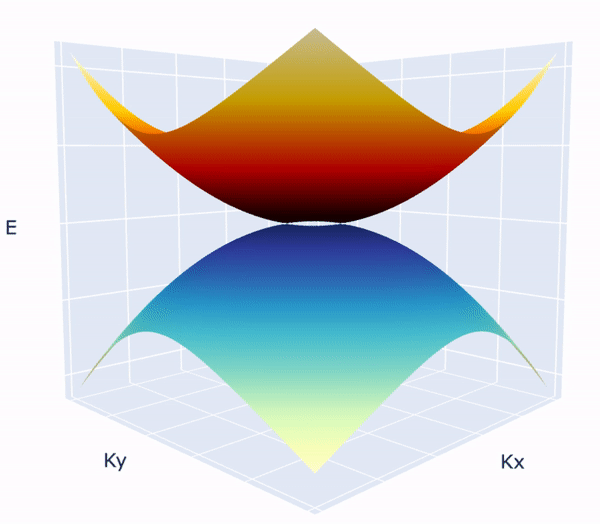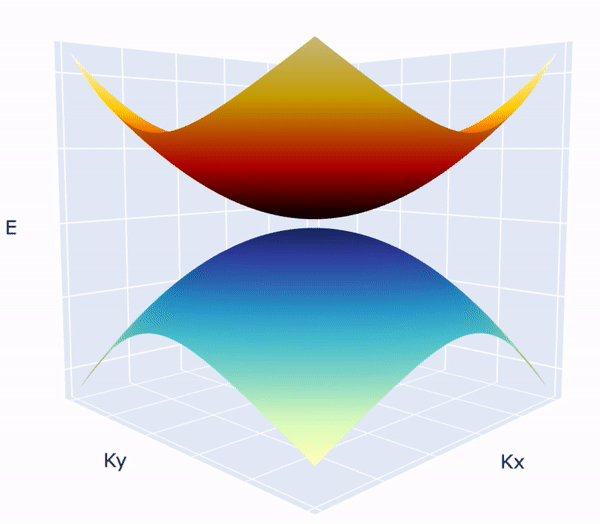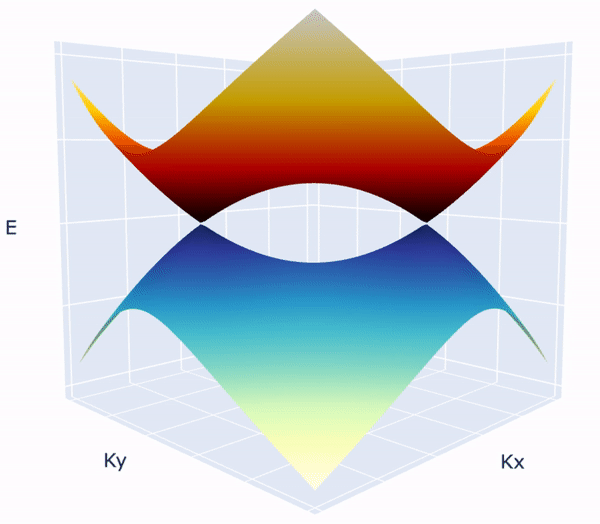
Non trivial quantum vacuum in Dirac annihilation: Surprisingly the vacuum ground state a quantum system after annihilating the dirac fermions becomes non trivial than a regular trivial gapped system. This non triviality is shown to stem from the *branch cuts* in the complex riemann sheets of ground state wave functions leading to something called "Obstructed Atomic Limit"
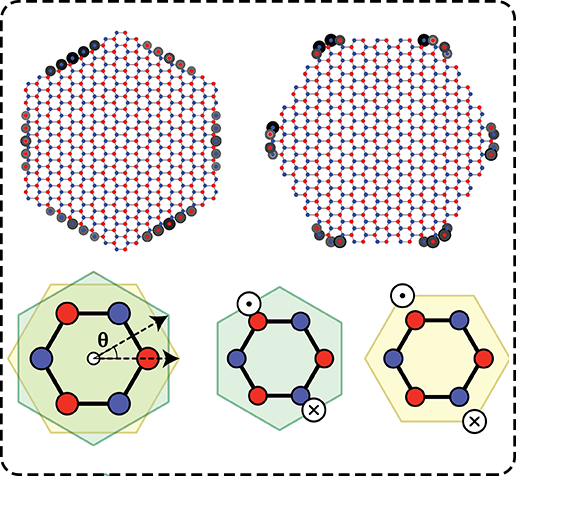
Buckled Honeycomb Group-V: Monolayer Sb usually exists in phosphorus like buckled layer which can be flatten out. Interestingly we how that one turns the system from a critical Nodal line to a dirac semi-metal and finally to a non trivial gapped system. More importantly, one can create and anihilate dirac cones of opposite winding number by buckling the system. further more we show that this is the first exammple of S-6 symmetric Higher Order Topological Insulator (HOTI).
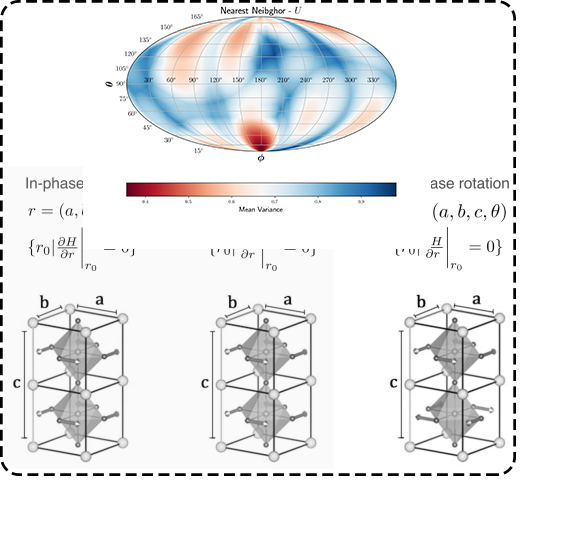
Pseudo-Spin dynamics of Halide perovskites: Metal Halide perovskites special class of systems which the next promising candidate for efficient solar cells. In this work, we try to understand the different phases this system can be in because of distortion by mapping them to a SO(3) anisotropic pseudo-spin Hamiltonian. This helped us predict a zoo of new meta stable structures that can possible be used for photo-chromatic applications. For ex, a transparent window that is also a solar cell which can be closed to stop all light by applying electric field. Read about it here
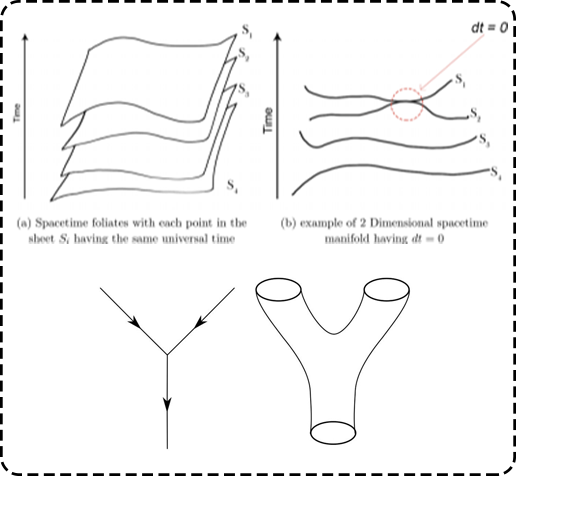
Classical Gravity and curvature in pure Space manifold: This research involved explaining the necessity of a time-like dimension even in the most simple case of non-relativistic theory, without which one cannot write consistent Lagrangian for gravitational fields.
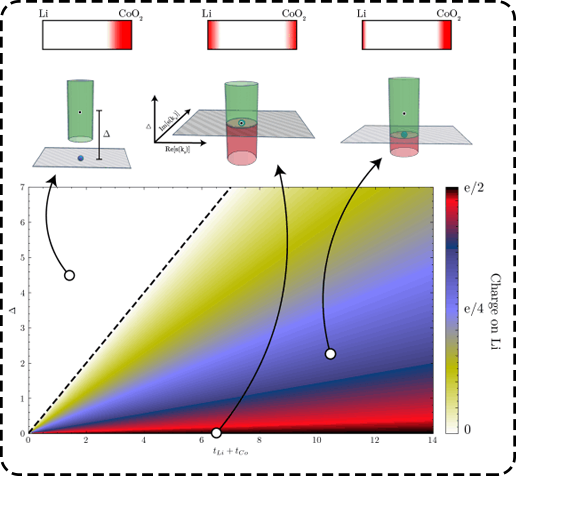
Topology and correlation in LiCoO2: Collaborating with experimentalists, while on a quest to make quantum 2-dimensional material CoO2 from LiCoO2 (the Chemistry Noble prize winning material), we discovered that the long studied and thought to be well understood LiCoO2 holds a key way to form 2 dimensional spin polarized electron gas which is topologically protected. And this could further possibly shine a new spin on a decade old unsolved problem - Unconventional superconductivity of NaxCoO2
Computer Science, Math, Music
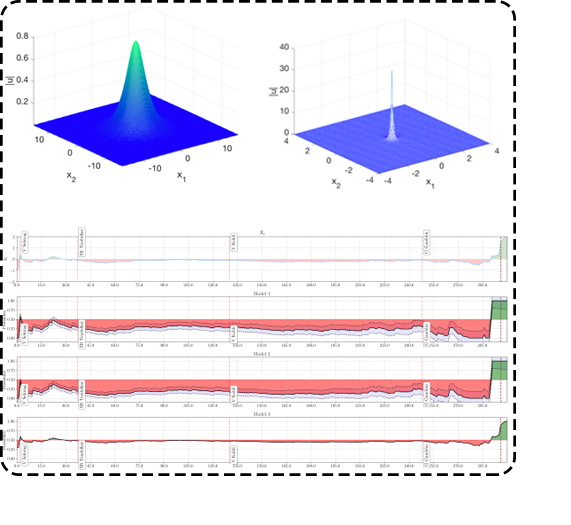
Stochastic theory of cricket: A new formalism for analyzing the progression of cricket game using Stochastic differential equation (SDE) is introduced. This theory enables a quantitative way of representing every team using three key variables which have physical meaning associated with them. This is in contrast with the traditional system of rating/ranking teams based on combination of different statical cumulants. Further more, using this formalism, a new method to calculate the winning probability as a progression of number of balls is given.Read about it here
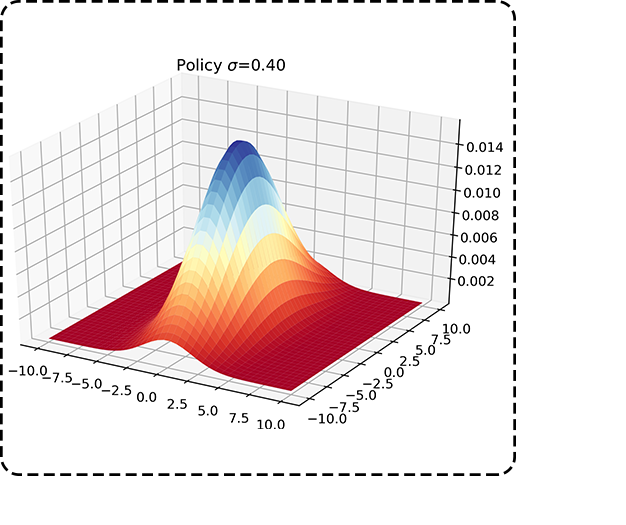
Information flow in elections: Using OU (Ornstein–Uhlenbeck) stochastic process, we model the flow and varience of information in an election and its effect on the outcome. Oftentimes, complicated policy stance is perceived as a negative effect on the outcome, here we show that there are points in phase space where a "confused" stance actually helps in party's favour. (pre-print to be published soon)
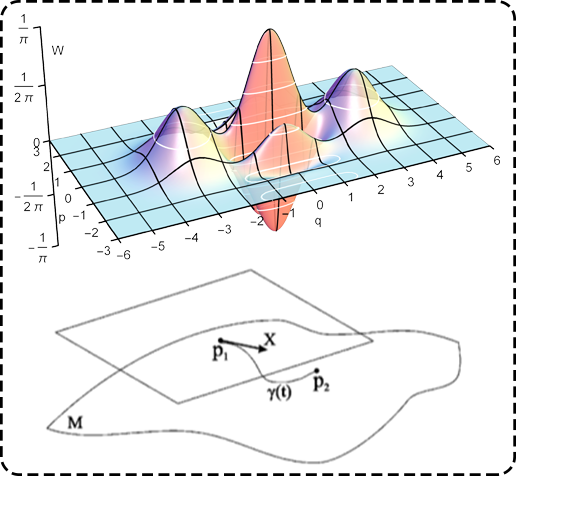
Mathematical modeling of Carnatic Ragas: Carnatic ragas have been one of the greatest fasciations of mine because of its esoteric nature. This complex entity is a dynamical evolution of frequencies sampled from a particular discrete set of frequencies but combined by a continuous function. We are trying to use a tensor product of discrete and continuous topology to model this complex system.
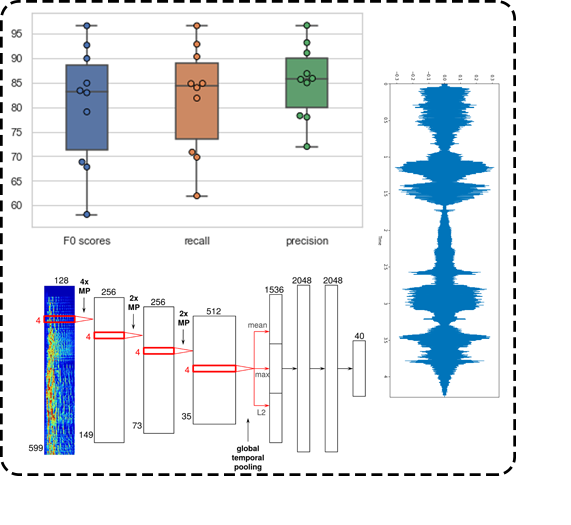
Machine learning in Carnatic music classification: To classify a Carnatic rage from a given set of recording is one of the most toughest computational problems because of the lack of fundamental understanding of what an object called raga is, yet humans do this classification with close to 100% accuracy. We are using K-nn along with SAX dimensional reduction to train and have compared the result with a LSTM+CNN neural net model.